Equation for a line in R2 | two points.

 


Example 1, equation of a straight line in form of ax + by + c = 0 is,

x - y + 0 = 0. Thus ( a = 1, b= - 1, c=0).

direction vector of line is (-b, a) = (1, 1).

line passing through point, (0, -0/1) = (0,0)

 =  (1,1)

Parametric form of the line passing through (x0,y0) with direction vector of (1,1)
x = xa + t d
y = ya + t d

For R3 parametric form is, 
thus, direction vector, can be defined in terms of angle.
alternatively, given angle with x line and passing through point, we can calculate equation for line.

Thus, equation of the line with angle of 45 degrees is,
x - y = c, and value of c can be from +/- infinity.

slope for above line is 1, with constant 0,
indicates y=x and line passing through origin.
line for the line: x-y =0.

line for the line: y = x + 2
when x is zero, y=2.

line for the line: y = x - 2
when x is zero, y is -2.




Reference










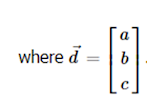
Comments

Post a Comment

Popular posts from this blog

Clear Understanding on Sin, Cos and Tan (Trigonometric Functions)

Image
  Clear Understanding on Sin, Cos and Tan (Trigonometric Functions) Trigonometry  (from  Ancient Greek   τρίγωνον  ( trígōnon )  'triangle', and  μέτρον  ( métron )  'measure')  is a branch of  mathematics  concerned with relationships between  angles  and side lengths of triangles.  All trigonometric formulas are divided into two major systems: Trigonometric Functions Trigonometric Identities In particular, the  trigonometric functions    relate the angles of a  right triangle  with  ratios  of its side lengths. Also, called as trigonometric rations. Trigonometric functions  are also known as  Circular or cyclic Functions. Trig functions  can be simply defined as the functions of an angle of a triangle. It means that the relationship between the angles and sides of a triangle are given by these trig functions. There are basically 6 ratios used for finding the ele...
Read more

Clear Understanding on Mahalanobis Distance

Image
  Clear Understanding on Mahalanobis Distance In multivariate/ multicharacteristics data, a measure of divergence or distance between groups in terms of  multiple characteristics is required. Lets consider, you are interested in measuring the difference (distance) between groups G1 and G2 (each of p-dimensional). A common assumption is to take the p-dimensional random vector X  , from each group, as having same variation about its mean within either group. The difference between the groups can be considered in terms of difference between mean vectors of X, in each group relative to the common within-group variation  (using common (pooled) covariance matrix). The most often used measure for multiple characteristics data is, Mahalanobis distance (Mahalanobis  Δ , where  Δ  is Uppercase Delta). The square of Mahalanobis distance is given by,  Δ 2 =  (µ 1 -µ 2 ) T Σ -1 (µ 1 -µ 2 ) or          Δ 2 =  (µ 1 -µ 2 ) ′ ...
Read more

Vignettes for Matrix concepts, related operations

  Geometric Transformations, compute the matrix of a rotation transformation and visualize it. Wolfram|Alpha Examples: Geometric Transformations (wolframalpha.com) Reference Change of Basis – GeoGebra Eigenvalues of a Matrix Calculator - Online Eigen Values λ Finder (dcode.fr) Eigenvectors of a Matrix Calculator (with Eigenvalues) - Online (dcode.fr) Matrix Visualization | Sarah Greer (sygreer.com)   Matrix visualizer (utexas.edu)  gives rotation by angle. Eigenvalue Calculator: Wolfram|Alpha (wolframalpha.com) Determinant Calculator: Wolfram|Alpha (wolframalpha.com)
Read more