Axis-aligned confidence ellipses
In general, the equation of an axis-aligned ellipse with a major axis of length 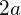 and a minor axis of length
and a minor axis of length 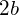 , centered at the origin, is defined by the following equation:
, centered at the origin, is defined by the following equation:
In our case, the length of the axes are defined by the standard deviations 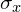 and
and 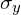 of the data such that the equation of the error ellipse becomes:
of the data such that the equation of the error ellipse becomes:where s defines the scale of the ellipse and could be any arbitrary number (e.g. s=1).
The question is now how to choose  , such that the scale of the resulting ellipse represents a chosen confidence level (e.g. a 95% confidence level corresponds to s=5.991).
, such that the scale of the resulting ellipse represents a chosen confidence level (e.g. a 95% confidence level corresponds to s=5.991).
The left hand side of equation (2) actually represents the sum of squares of independent normally distributed data samples, cov is zero. The sum of squared Gaussian data points is known to be distributed according to a so called Chi-Square distribution. A Chi-Square distribution is defined in terms of ‘degrees of freedom’, which represent the number of unknowns. In our case there are two unknowns, and therefore two degrees of freedom.
For example, using this probability table we can easily find that, in the 2-degrees of freedom case:
Therefore, a 95% confidence interval corresponds to s=5.991. In other words, 95% of the data will fall inside the ellipse defined as:
The error ellipse show by figure 2 can therefore be drawn as an ellipse with a major axis length equal to 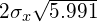 and the minor axis length to
and the minor axis length to 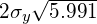 .
. Arbitrary confidence ellipses
Reasoning of scale of ellipse holds if we temporarily define a new coordinate system such that the ellipse becomes axis-aligned, and then rotate the resulting ellipse afterwards.
In other words, whereas we calculated the variances 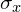 and
and 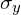 parallel to the x-axis and y-axis earlier, we now need to calculate these variances parallel to what will become the major and minor axis of the confidence ellipse.
parallel to the x-axis and y-axis earlier, we now need to calculate these variances parallel to what will become the major and minor axis of the confidence ellipse.
In the case of arbitrary correlated data, the eigenvectors represent the direction of the largest spread of the data, whereas the eigenvalues define how large this spread really is.
Thus, the 95% confidence ellipse can be defined similarly to the axis-aligned case, with the major axis of length 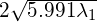 and the minor axis of length
and the minor axis of length 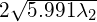 , where
, where 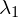 and
and 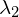 represent the eigenvalues of the covariance matrix.
represent the eigenvalues of the covariance matrix.
Reference
- How to draw an error ellipse representing the covariance matrix? (visiondummy.com)
- What are eigenvectors and eigenvalues? - Computer vision for dummies (visiondummy.com)
- A geometric interpretation of the covariance matrix (visiondummy.com)
![]() and
and ![]() parallel to the x-axis and y-axis earlier, we now need to calculate these variances parallel to what will become the major and minor axis of the confidence ellipse.
parallel to the x-axis and y-axis earlier, we now need to calculate these variances parallel to what will become the major and minor axis of the confidence ellipse. ![]() and the minor axis of length
and the minor axis of length ![]() , where
, where ![]() and
and ![]() represent the eigenvalues of the covariance matrix.
represent the eigenvalues of the covariance matrix.






Comments
Post a Comment